2022年国家公务员考试《行测》模拟卷④（副省级）69

2021-09-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

容斥问题。根据题意，假设三项比赛都参加的有x人，则只参加演讲和诗朗诵但是未参加作文比赛的有26-x人，只参加演讲和作文但未参加诗朗诵比赛的有18-x人，只参加诗朗诵和作文但是未参加演讲比赛的有15-x人，再假设只参加作文比赛的有y人，则参加演讲比赛的有2y人，故只参加演讲比赛的人数为2y-x-（26-x）-（18-x）=2y+x-44。如下图所示：

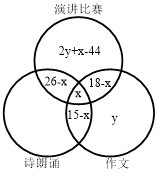
根据题意，没参加诗朗诵的有70人，也即2y+x-44+18-x+y=70，解得y=32，则只参加演讲比赛的人数为2×32+x-44=20+x。想要只参加演讲比赛的人数最少，则需要让x有最小值，根据题意，有人参加三项比赛，也即x的最小值为1，因此只参加演讲比赛人数的最小值为20+1=21人。

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。