2012年国家公务员考试《行测》真题卷62

2011-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

行程问题。题干、选项都是倍数、百分数、比例，不涉及具体的数值，可考虑赋值法求解。

根据题意可知，“甲跑步的速度是乙步行速度的2.5倍”，赋值乙的速度为2，则甲的速度为5；由于甲“每跑半小时都需要休息半小时”，每半小时甲追上乙5×0.5-2×0.5=1.5；由于乙连续运动不休息，则每一小时甲追上乙5×0.5-2×1=0.5；由于甲比乙晚出发2小时，则追及路程为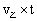=2×2=4；由于最后的追及过程甲并不需要休息，则在此之前的追及时间为（4-1.5）÷0.5=5h，最后1.5的路程仅需要追及半小时，则总追及时间为5+0.5=5.5h，则9:00出发5.5h后追上的时间为14:30。

因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。