2019年国家公务员考试《行测》真题卷（副省级）67

2018-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】
概率问题。根据“甲每局获胜的概率是乙每局获胜概率的1.5倍”，设乙每局获胜的概率为x，则甲获胜的概率为1.5x，可得1.5x+x=1，解得x=0.4，即甲每局获胜的概率为0.6，乙每局获胜的概率为0.4。根据“5局3胜”，逐个对选项进行计算：

A项：比赛在3局内结束，若甲连胜3局，概率为0.6×0.6×0.6=0.216；若乙连胜3局，概率为0.4×0.4×0.4=0.064。故A项总概率为0.064+0.216=0.28。

B项：乙连胜3局获胜，有三种情况：①乙第1、2、3局连胜，概率为0.4×0.4×0.4=0.064；②乙第2、3、4局连胜，概率为0.6×0.4×0.4×0.4=0.0384；③乙第3、4、5局连胜，概率为0.6×0.6×0.4×0.4×0.4=0.02304；故B项总概率为0.064+0.0384+0.02304=0.12544。

C项：甲获胜且两人均无连胜，只有一种情况，即甲第1、3、5局获胜，乙第2、4局获胜，概率为0.6×0.4×0.6×0.4×0.6=0.03456。

D项：乙用4局获胜，则第四局必然是乙获胜，且前三局中乙有两局获胜，因此概率为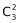×0.4×0.4×0.6×0.4=0.1152。

比较可知，A项概率最大。

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。