2020年上半年全国事业单位联考《职测》（A类）50

2021-01-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

行程问题。

根据题意可知乙车在上坡、平路和下坡时，速度分别为甲车的0.5、1和2倍，可赋值甲的速度为1，则乙上坡速度为0.5、平路速度1、下坡速度2。

第一次相遇点为D，甲从A点到B点速度为1，乙从A点到C点是平路速度为1，甲和乙同时分别到达B、C，甲由B到C点速度为1，乙有C到B点速度为0.5，根据时间相同时路程之比等于速度之比，可知BD=2CD，即BD=。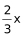

从D到第二次相遇点E，乙由D到B点，路程是甲的2倍，速度是甲的一半，所用时间为甲的4倍，因此当乙到达B点时，甲到达A点。甲由A到B速度是1，乙由B到A下坡速度是2，根据时间相同时路程的比等于速度的比，可知BE=2AE，即BE=。

故y为道路长度最短=BD+BE=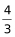x，即y≥1.3x。

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。