2019年下半年浙江省事业单位统考《职测》65

2020-01-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

第一步，拥堵期间行驶速度为40千米/小时。若现全程用时45分钟即0.75小时，假设在非拥堵期间行驶时间为a小时，拥堵期间行驶时间为b小时，满足：a+b=0.75，80a+40b=40。解得a=0.25，b=0.5。

第二步，若全程用时不超过45分钟，则非拥堵行驶时间不少于0.25小时，拥堵时间不超过0.5小时，即需要在拥堵前至少0.25小时出发或在拥堵剩余时间不超过0.25小时出发。

设x时出发，则6≤x≤9，y时开始拥堵，7≤y≤8，拥堵时段为（y，y+2），x.y取值范围为下图长方形所示区域。若全程用时不超过45分钟，则y-x≥0.25，y+2-x≤0.5。分别可整理为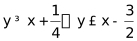：，满足区域如下图阴影部分所示。

第三步，阴影部分面积为：[（6.75-6）+（7.75-6）]×（8-7）×0.5+（9-8.5）（7.5-7）×0.5=1.375。

长方形面积为：（9-6）（8-7）=3，题目所求概率为1.375÷3=45.8%。

因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。