2020年9月福建省事业单位考试《综合基础知识》70

2021-01-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

因为△ABC为等腰直角三角形，所以∠HEC＝90°，∠C＝45°，故三角形HEC为等腰直角三角形。
由两直线相交，对顶角相等。∠EHC和∠GHD为对顶角，相等，均为45°。
即∠DGH＝180°-∠GHD-∠D＝180°-45°-45°＝90，即三角形DHG为等腰直角三角形。
所以△ABC～△HEC～△HGD。∠F＝∠C＝45°，∠FB1＝90°，∠FB1＝45°，故三角形IBF为等腰直角三角形。

三角形ABC为等腰直角三角形，所以AB＝BC＝9cm，BE＝BC-EC＝9-3＝6cm，BF＝EF-BE＝9-6＝3cm＝EC。即∠HEC≌△1BF，S△1BF＝（1BxBF）/2=（3x3）/2＝4.5cm2。EC＝3cm，三角形HEC为等腰直角三角形，即HE＝3cm，且△ABC和△DEF全等，AB＝BC＝DE＝EF＝9cm。即DH＝DE-HE＝9cm-3cm＝6cm；三角形DGH为等腰直角三角形，DG²＋GH²＝DH²＝36，DG＝GH，得DG＝GH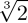＝cm，S△DGH＝（DG×GH）/2=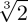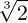（×）/2＝9cm²

即S_阴＝S△DEF - S△IBF - S△DGH=(9X9)/2-4.5-9＝27cm²。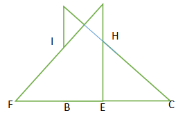

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。