2019年5月福建省事业单位考试《综合基础知识》57

2020-01-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

第一步，根据题意可知，此题考察同余特性，即“和与余数的和同余”“差与余数的差同余”“积与余数的积同余”。

第二步，因为2001除以13的余数为12，所以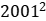处于13的余数为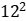=144；又因为144除以1的余数为1，所以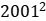除以13的余数为1；则可以推出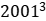除以13的余数为1×12=12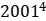，除以13的余数为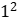=1。根据以上结果可以发现，2001的奇数次方除以13的余数为12，2001的偶数次方除以13的余数为1，因此2001的2003次方除以13的余数为12。

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。