2016年山东省公务员考试《行测》真题卷65

2016-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

几何问题。根据一笔画规律可知，当时奇点为0或2时，可一笔画完，其他情况则至少需要（奇点个数÷2）笔画完。由图可知，共有4个奇点（A、C、E、F），则至少需要2笔画完全图。要求行进的距离最少，则重复路径应尽量少，从一个奇点出发，需要重复走某一段路，走到另一个奇点，才能走完全程，则两个奇点可得去C和F（或A和E）。最短路径为E-A-D-E-B-D-F-B-C-F-C-A，最短距离为菱形周长+两条对角线+DE+BF+CF。根据题意，菱形变成为800÷4=200米，又因为△ABD、△BCD为正三角形，DE、BF分别与AB和CD垂直，则E、F分别为AB、CD的中点，则AE=CF=200÷2=100米，DE=B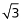F=CF=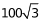米，AC=2BF=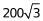米。故最短距离为800+200+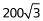++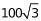+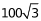100=1100+米。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。