2016年山东省公务员考试《行测》真题卷63

2016-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

行程问题。方法一：根据题意可得，甲车做初速度为40公里/小时，加速度为2公里/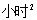的匀加速运动，乙车初速度为50公里/小时，做加速度为-2公里/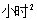的匀减速运动。根据公式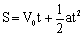：，其中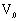为初速度，a为加速度，则甲乙两车行驶的路程差为，根据二次函数图像理论，可得路程差的函数图像为一条开口向下的抛物线，当t=2.5时，路程差有最大值，为12.5公里。

方法二：根据题意分析可得，甲乙两车同时同地同向出发，乙车做初速度较大的减速运动，甲车做初速度较小的加速运动，则两车之间距离应为先增大，且当甲、乙两车速度相同时达到最大，而后甲车速度超过乙车，两车之间距离则不断减小，直至甲车追上乙车，再超过乙车，车间距离又开始不断增大。

设x小时后两车速度相等，可列：40+2t=50-2t，解得t=2.5，即2.5小时后两车距离最大。此时，甲、乙两车的速度均为45公里/小时，两车间距离达到第一次最大值为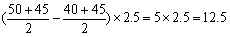公里。

而后甲车速度超过乙车，两车之间距离则不断减小。则当甲车速度达到50公里/小时，乙车降到40公里/小时时，两车行驶路程相同，即甲车追上乙车。此过程需要5小时，故8点出发，12点前两车最大距离为12.5公里。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。