2021年江苏省公务员考试《行测》（C卷）59

2021-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

排列组合问题。

方法一：先分类：

思路说明：甲不去A社区，甲去了C还是去了非C，对丙来说是有影响的，而且丙是否去了C，对丁又是有影响的，所以先不考虑甲。先考虑丙是否去了C社区，若丙去了C，情况是很简单的，此后再去考虑丙没有去C会如何将会简单一些。故先分类丙是否去了C社区。

一：丙去了C社区，则丁会去D社区，甲不去A社区，只能去B社区，乙则只能去A社区，只有一种情况。

二：丙未去C社区。（思路说明：甲和丙会相互影响，若甲去了C，下一步丙有3个社区可以选，但若甲去了B或D，丙则只有两个社区可以选择，所以需要再次分类。）

再次分类：

（1）若甲去了C社区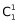，丙有三个社区可选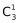，乙、丁剩下两个社区随机选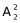，该二次分类情况数有；

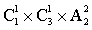（2）若甲没去C社区，可选B或D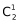，丙有两个社区（非C社区非甲所选社区的另外两个）可以选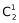，乙、丁剩下两个社区随机选，该二次分类情况数有；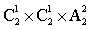

则总的情况数有：1+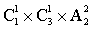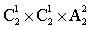（+）=1+（6+8）=15。

方法二：甲不去A社区，甲只能从B、C、D三个社区中选一个有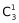种，如果对乙、丙、丁三人没有其他限制条件，则剩下乙、丙、丁三个人全排列有种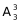，总共有种，但题目对剩下三人有限制条件，所以总数应小于18，只有A项15满足。

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。