2021年江苏省公务员考试《行测》（B卷）87

2021-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

本体考查四面体折叠，首先在左侧平面展开图中进行标记，如图：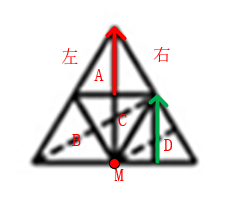

A项，该项中的两个面都有一条实线和一条虚线，左侧展开图中类似的面只有C面和D面，选取左侧展开图中的D面，沿实线画一个绿色的箭头，则箭头的左下角对应的顶面M是D面中虚线的端点。以同样的方式在A项立体图形中画箭头，如图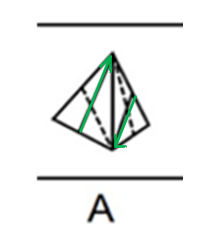：发现不论哪个面的左下角顶点都不是虚线的端点，故可以断定，这两个面都不是D面，所以A选项不能从左侧展开图折叠得来，排除；

B项，该项立体图形中的右侧面对应左侧展开图中的A面，在左侧展开图中的A面中标上箭头，如图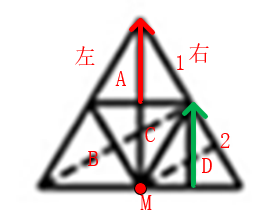：其中D面位于A面中箭头的右侧，并且边1和边2重合。将该项中的右侧面标上箭头如图所示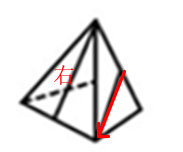：该项的右侧面对应展开图中的D面，因此该项能够折叠成，保留；

C项，该项的左侧面对应展开图中的A面，同样将其标上箭头，如图所示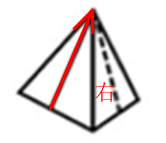：箭头的右侧面对应的是B面，而展开图中的红色箭头的右侧面是D面，故不能折成，排除；

D项，该项立体图形的左侧面对应展开图中的B面，沿着B面中的虚线画箭头，如图所示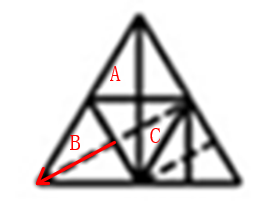：则箭头的尾部对应C面，箭头尾部的左侧顶点对应C面中黑色线条的端点。将该项立体图形的左面同样标上箭头，如图所示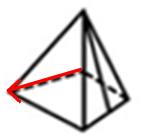：但箭头尾部的右侧顶点对应的是C面中黑色线条的端点。故不能折成，排除。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。