2018年山西省421联考《行测》卷61

2018-05-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】
几何问题。本题所求为小郑最少用了多少块瓷砖，瓷砖总数量=所需题中图形的数量×每个图形需要的瓷砖数量，每个图形所需的瓷砖数量固定为10，所以只需要将所需题中图形数量最少即可。观察该图形的长、宽与单独瓷砖的长、宽的关系，如图：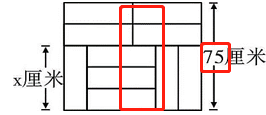

可知5个瓷砖的宽等于75厘米，所以一个瓷砖的宽为75÷5=15厘米，所以一个瓷砖的长为75-2×15=45厘米，即该图形的长为45+3×15=90厘米，宽=75厘米；因为最终需要把一定数量的题中图形拼成正方形，正方形边长相等，即设需要该图形n个长，m个宽，根据最终正方形边长相等可列等式90n=75m，n：m=5：6，又因为不可能单独出现一个长或者宽，所以必须使得最终长和宽出现的数量相等，且最小，那么取n、m最小公倍数为30，所以需要题中图形30个拼成正方形，总瓷砖数量最少=30×10=300块。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。