2019年辽宁省公务员考试《行测》真题卷64

2019-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

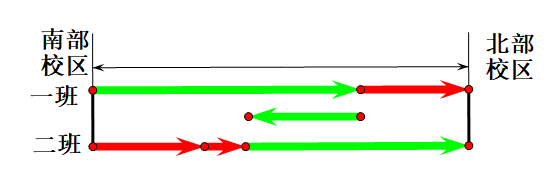
行程问题。如下图所示，绿色代表坐车，红色代表步行。在一班下车之前，两个班所用的时间一致，故此时的路程之比等于速度之比，即为40∶4=10∶1。即此时一班坐车走了10份，二班步行走了1份。在车返回去接二班的过程中，空车行驶时间和二班步行时间依然相同，则空车和二班的路程之比等于速度之比，即为50∶4=25∶2。此时空车行驶路程和二班步行的路程等于车掉头前一班和二班的路程差，即为10−1=9份。所以空车和二班相遇时，二班走过的路程为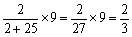份。则二班步行的总路程为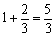份。由于两个班同时出发，同时到达，所以两个班坐车的路程应相等，步行的路程也应相等。故一班步行的路程=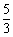份，坐车路程为10份，所以两个校区总路程为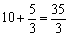份。则二班步行的路程占比为。

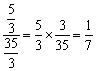因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。