2019年江西省公务员考试《行测》真题卷70

2019-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

几何问题。

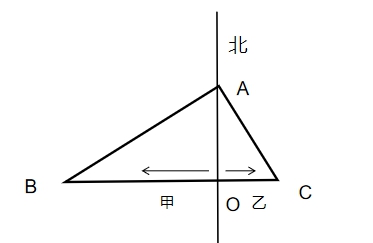
根据“乙部晚半小时由大本营往东行进，速度比甲部慢”可知OB>OC,所以∠ABC=30°，直角三角形CAB中，=tan30°=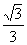，所以AB∶AC=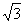∶1。已知两部同时调整方向并同时到达集合地，则运动时间相同。因为路程=速度×时间，时间相等，则甲部路程∶乙部路程=甲部速度∶乙部速度=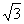∶1。已知甲部的速度为60千米/小时，那么乙部的速度就是千米/小时。

∠ABC=30°，∠BAC=90°，则∠ACB=60°，∠CAO=30°。直角三角形AOB中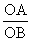，=tan30°=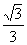，则OB∶OA=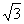∶1；直角三角形AOC中，=tan30°=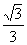，则OA∶OC=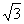∶1，则OB∶OC=3∶1。

设甲由O点到B点所用时间为t，那么OB=60t，OC=20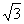（t-0.5），因为OB∶OC=3：1，则60t∶20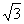(t-0.5)=3，解得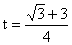，则。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。