2017年四川省公务员考试《行测》真题卷（下半年）43

2017-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

几何问题。根据题干可知，倾斜后液体没有流出，则倾斜前后圆柱体的空余部分体积相等。设直立时空余部分的高为h1，倾斜后空余部分的高为h2，圆柱体的底面积为S，则S×h1=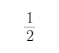S×h2，化简可得h2=2h1。已知“4为高的圆柱体内装了高度为3的液体”，则h1=4－3=1，h2=2×1=2。已知圆柱体的底面半径为1，则AC=2=h2，所以△BAC为等腰直角三角形，∠ABC=45°，则倾斜角为45°。

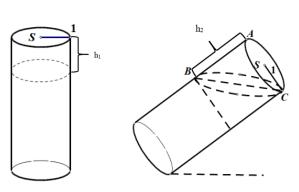
因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。