2019年浙江省公务员考试《行测》真题卷（B类）62

2019-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

概率问题。从三种不同包装中随机拿4盒，可知总的情况有拿出来的每一个盒子都有三种规格可选，所以一共有3×3×3×3＝81种拿法。满足题目的拿法我们可以列表来看，由于最后拿的苹果要是偶数，所以根据奇偶性得8个一盒规格的要拿偶数盒，又根据题目说拿的苹果数要大于20个，所以8个一盒规格的不能拿0盒，所以拿法如下表。

8	5	3
4盒	0盒	0盒
2盒	2盒	0盒
2盒	1盒	1盒
2盒	0盒	2盒

①4盒8个装的情况数为1种，即（8，8，8，8）；

②8个和5个装各2盒的情况数为6种，即（8，8，5，5），（5，5，8，8），（8，5，5，8），（5，8，8，5），（8，5，8，5），（5，8，5，8）；

③2盒8个、1盒5个和1盒3个装的情况数为12种，分两种情况讨论，两个8在一起，捆绑法可得有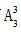=6种；两个8不在一起，即插入到5和3之间，插空法可得有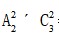=6种，该情况共计6+6=12种；

④8个和3个装各2盒的情况数应和8个和5个装各2盒的情况数一致，也为6种。则满足条件的总情况数为1+6+6+12=25（种），所求概率为

。

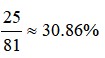因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。