2019年浙江省公务员录用考试《行测》真题（A类）73

2019-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

排列组合问题。结合选项本题总情况数相对较少，适合枚举法解题，方式如下：

第一类：周二、周四、周六上课，则有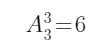种情况。

第二类：周三、周四、周六上课，因英语和会计不能在连续的两个晚上，用总情况数减去英语和会计连续的情况，则有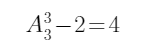种情况。

第三类：周三、周五、周六上课，因英语和会计不能在连续的两个晚上，同理有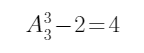种情况。

第四类：周三、周五、周日上课，则有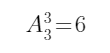种情况。

所以总共有6+4+4+6=20种情况。

因此，答案为B。

方法二：先考虑休息日不连续，由插空法可知共有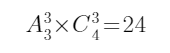种方式。

这其中，如果英语和会计是连续上课的话，由捆绑法可知，共有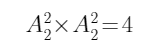种方式。

所以既满足休息日不连续，又满足英语班和会计班不连续共有24-4=20种方式。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。