
2017年浙江省公务员考试《⾏测》真题卷(A类)41

【思路】
几何问题。
方法一:根据题意可知,三角形ABC为直角三角形,且∠B为直角,甲走的距离为AC,乙走的距离为BC,由于同时出发同时到达,时间相同,速度之比与路程成正比,所以AC=2×BC=2r,又因为半圆面积为54π,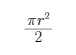 =54π,所以r2=108,所以AC2=(2r)2=4r2=4×108,BC2=r2=108,所以AB2=AC2-BC2=(4-1)×108=3×108,所以AB=18米。
=54π,所以r2=108,所以AC2=(2r)2=4r2=4×108,BC2=r2=108,所以AB2=AC2-BC2=(4-1)×108=3×108,所以AB=18米。
因此,答案为D。
方法二:根据题意可知,三角形ABC为直角三角形,且∠B为直角,甲走的距离为AC,乙走的距离为BC,由于同时出发同时到达,时间相同,速度之比与路程成正比,所以AC=2×BC,可知三角形ABC为30°的直角三角形,三边比例关系为BC∶AB∶AC=1∶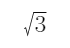 ∶2,又因为半圆面积为54π,
∶2,又因为半圆面积为54π,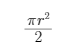 =54π,所以r2=108,且AC=2×BC,其中AC为直径,则BC长为半径即BC=r=6
=54π,所以r2=108,且AC=2×BC,其中AC为直径,则BC长为半径即BC=r=6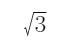 ,则AB=
,则AB=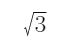 BC=
BC=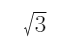 ×6
×6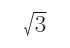 =18米。
=18米。
因此,答案为D。
大家都在搜
 换一批
换一批
 换一批
换一批
备考工具
相关搜索
热门搜索

 上岸鸭公考
上岸鸭公考






