2018年四川421联考《行测》卷55

2018-05-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

简单计算。已知“10个相同的盒子中分别装有1～10个球，任意两个盒子中的球数都不相同”，则10个盒子的球数分别为1、2、3......10，构成公差为1的等差数列。等差数列前n项和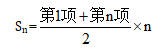，所以10个盒子里一共有小球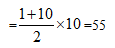个。设第一次取出的小球数为X，最后剩下的盒子中有Y个小球，已知“每次取出的盒子中的球数之和都是上一次的3倍”，则第二次取出的小球数量为3X，第三次取出的小球数量为9X。最后剩下盒子中的小球数=总共的小球数－每次取出的小球数，则Y=55－（X＋3X＋9X）=55－13X，可以转化为55－Y=13X，因为X一定为整数，所以55－Y为13的倍数，代入选项只有D符合。

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。