2017年浙江省公务员考试《⾏测》真题卷（A类）39

2017-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

行程问题。根据题目表述，有两个均匀变化的量影响水库内的蓄水量，符合“牛吃草”模型。设每个水闸每天放水量为1，每天流入水库的水量为x，根据题干，到达警戒水位所需水量=（x-2）×3=（x-3）×4，解得x=6，即每天进水量为6，则到达警戒水位所需水量为（6-2）×3=12。未来7天流入水库的水量将比之前多20%，即每天进水量变为6×（1+20%）=7.2。假设需打开n个水闸可以保证7天内水量低于警戒水位，则（7.2-n）×7<12，得n>7.2-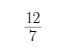≈5.5，则需要至少打开6个水闸。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。