2019年江苏省公务员考试《行测》（A卷）49

2019-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

概率问题。本题可以等效于在一条长度为1的线段上插入两个截点，能满足截成的三条线段中最短的两条的和大于最长边。

第一个截点可以确定第一条边的长度，由于第一条边的长度必须小于后面两条边的和，所以第一个截点可取的位置范围如图所示：

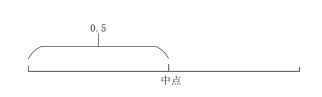
所以第一个截点的取值范围为0~0.5。

第二个截点可以确定第二条边的长度，由于第二条边和第一条边的长度和应大于第三条边，所以第二个截点的位置应比中点偏右。第一条边和第三条边的长度和应大于第二条边，所以第二个截点应比0.5+x偏左。即第二个点的取值范围应为0.5~0.5+x。

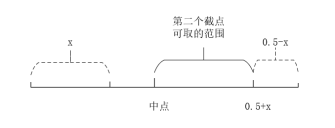
画函数图像来解决概率问题。x代表第一个截点的取值范围，y代表第二个截点的取值范围。

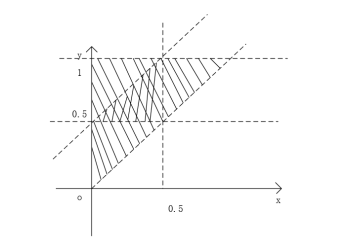
能构成三角形的部分占整体的。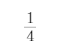

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。