2018年江苏省公务员考试《行测》（A卷）48

2018-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

概率问题。

方法一：根据题意，可得要将四名警察分到3个专案组，则分为一个2人组和两个1人组，总情况为从4人中选取2人分配到2人组，其余2人各自在1人组，共有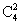=6种情况，符合条件的情况为来自同一派出所的警察不在同一组，则2人组的成员来自不同的派出所，共有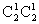=4种情况，则来自同一派出所的警察不在同一组的概率是。

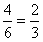因此，答案为A。

方法二：由题意可知，4名警察分到3个专案组，必有2人同组，其他2人各自一组。从4人中选出2人，有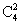=6种方法；随机安排到3个专案组工作，每种分组情况均有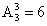种安排方法。所以将4名警察随机安排到3个专案组工作共有6×6=36种情况。

从反面考虑，若同一派出所的警察在同一组，则其中一个派出所的2名警察被安排到一个专案组，另外一个派出所的2名警察分别安排到另外2个专案组，所以共有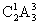=12种情况。

因此，来自同一派出所的警察不在同一组的概率1－。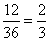

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。