2020年安徽822联考《行测》卷14

2020-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

几何问题。设甲乙丙丁分别为ABCD，根据题意可得下图，

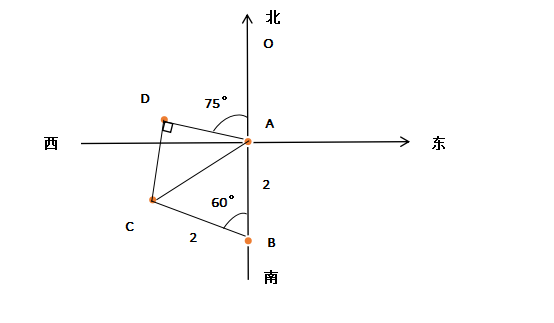
已知AB=BC=2，∠ABC=60°，则△ABC为等边三角形，则AC=2，∠CAB=60°；

已知∠OAD=75°，则∠DAC=18

0°－∠OAD－∠CAB=180°－75°－60°=45°；

已知“丁与甲、丙的距离相等”，即DA=DC，则△ADC为等腰三角形，已知∠DAC=45°，则∠DCA=∠DAC=45°，∠CDA=90°，所以△ADC为等腰直角三角形；

在为等腰直角三角形ADC中，AC=2，则DA=DC=。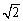

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。