2019年四川420联考《行测》卷48

2019-05-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

经济利润问题。

方法一：由题意可设A款服装的进价为4x，B款服装进价为4x×75%＝3x，定价为3x×1.6＝4.8x，则A款服装定价为4x＋（4.8x－3x）×2＝7.6x。某日商店以定价销售A款服装总销售额超过2500元，设当日的销售量为y，则y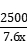＞，x值越大，y值越小，要使得当日卖出件数最少，则x取最大值。又因为购入100多件A款服装，且进价为整数元，总进价为1万元，则总件数为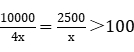，x最大整数取值为20，此时y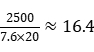＞，则至少需要卖出17件。

因此，答案为C。

方法二：由题意可知A款服装总件数为100多件，且进价为整数元，总进价为1万元，设A款服装单件进价为x，则A款服装总件数为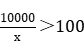，x＜100，且为整数。

若要使得当天销售的A款服装越少，则进价应越高。则可得出A款服装进价最大取值为80元，共有125件。B款服装进价为80×0.75＝60（元），B款服装利润＝定价－进价＝（1.6－1）×60＝36（元），则A款服装的利润为36×2＝72（元），因此A款服装的定价为72＋80＝152（元），销售额未2500元时，卖出了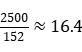，则至少需要卖出17件。

因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。