2017年江苏省公务员考试《行测》（A卷）39

2017-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

排列组合问题。

方法一：要求2名超过50岁的员工不在同组，则有两种情况：

①两个3人组各有一名，则先从剩余的6人中选两人跟一名超过50岁的员工组成3人组，再从剩余的4人中选两人跟另一名超过50岁的员工组成另一个3人组，剩余2人组成2人组，共有 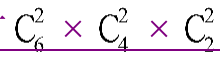=90种；

②3人组、2人组各有一名，则先确定哪名超50岁的员工在3人组，然后从剩余的6人中选两人跟一名超过50岁的员工组成3人组，再从从剩余的4人中选三人组成另一个3人组，最后剩余1人与另一超过50岁的员工组成2人组，共有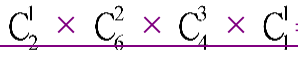=120种；

综上，共有90+120=210种。

因此，答案为D。

方法二：如果不考虑超过50岁的员工是否在一组，共有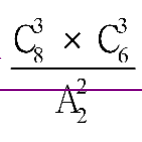=280种分组方式，如果50岁的员工在同一组，则有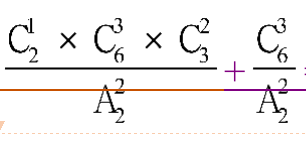=60+10=70种，所以50岁的员工不在一组的分法共有280-70=210种。

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。