国家公务员

上岸鸭公考> 国家公务员> 考试题库> 行测题库> 行测试题>

2019年国家公务员考试《行测》真题卷（副省级）61

2018-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】
简单计算。根据“发现如果增加5盆，就能摆成实心正三角形”，设组成的实心正三角形每个边有n个花盆，则原有花盆数量为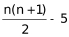。根据“如果减少4盆，就能摆成每边多于1个花盆的实心正方形”，组成一个实心正方形，需要花盆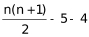= 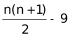盆。因为正方形，所以该数是平方数。想最外层花的盆数少，n的值应尽可能小，取n=2、3、4......的平方值代入进行验证。

若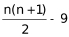=4，n为非整数，排除。

若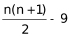=9，n为非整数，排除。

若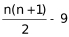=16，n为非整数，排除。

若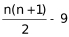=25，n为非整数，排除。

若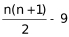=36，解得n=9，满足。

则原有花盆最少为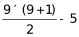=40盆。设实心矩形方阵长边放x盆花，宽边放y盆花，则x×y=40。要让最外层的花盆数最少，即2（x+y）-4（方阵四个角重复计算）最少。当积一定时，x与y越接近其和越小，故当x=8、y=5时，其和最小。花盆总数应为2×（8+5）-4=22盆（四个角重复计算）。

因此，答案为D。

版权声明：1、凡本网站注明“来源上岸鸭公考”的所有作品，均为本网站合法拥有版权的作品，未经本网站授权，任何媒体、网站、个人不得转载、链接、转帖或以其他方式使用。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。

上一篇

2019年国家公务员考试《行测》真题卷（副省级）60

2019年国家公务员考试《行测》真题卷（副省级）60

大家都在搜

换一批

备考工具

CopyRight © 2006-2024 上岸鸭公考 www.gwy.com All Right Reserved