2016年下半年B类待修53

2017-01-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

因为每个月初进货，且月初库存会包括上个月结余，所以每个月最大库存量应该出现在月初。因此，需要根据月初的进货量及本月销售量得到每月库存，依此类推寻找规律，找到库存最大量将无限接近多少吨。
用到等比数列相关公式：等比数列{a_n}的通项公式为：a_n=a₁×q^(n-1)，前n项和公式为：S_n= a₁(1-qⁿ)/(1-q) 。

由题，刚开始无库存，第一个月初进货400，卖出80%，则第一个月初库存最大最为400，月末库存量为：400×20%；
第二月初进货400，则此时库存为400+400×20%，此时当月库存量最大，月末卖出库存量的80%后，月末库存量为（400+400×20%）×（1-80%）=400×20%+400×（20%）²；
第三月初进货400，则此时库存为400+400×20%+400×（20%）²，此时当月库存量最大，月末卖出库存量的80%后，月末库存：[400+400×20%+400×（20%）²]×（1-80%）=400+400×20%+400×（20%）²+400×（20%）³
……依次类推
可知第n个月初的库存量为：400+400×20%+400×（20%）²+……400×（20%）^n-1，此时当月库存量最大，又合并同类项并根据等比数列求和公式可得：400+400×20%+400×（20%）²+……400×（20%）^n-1=400（1+0.2+0.2²+……+0.2^n-1）=400×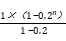=500×（1-0.2ⁿ），当n趋向无穷大时，月初库存量最大量将无限接近500吨。

因此，答案为B。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。