2017年深圳市公务员考试《行测》真题卷61

2017-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

最值问题。要想使第10场比赛得分尽可能少，即在总分数尽可能少的情况下，使其余9场比赛得分尽可能多。

设小明第10场比赛得分为x分，则x=前10场总分-前5场总分-第6至9场总分=前10场总分-前5场总分-（23+14+11+20）=前10场总分-前5场总分-68；要使x最少，则前10场总分要尽量小，且前5场总分要尽量大。又因为第6至9场的平均分为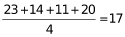分，根据混合平均原理可知，前9场的平均分居于前5场的平均分和第6至9场的平均分之间，由于前9场的平均得分比前5场的平均分高，则前5场的平均分<第6至9场的平均分，即前5场的平均分<17分，则前5场总分<17×5=85分，故前5场总分最大为84分。故x最少为：181-84-68=29分，即第10场比赛最少要得29分。

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。