2021年江苏省公务员考试《行测》（A卷）60

2021-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

统筹规划问题。所需要等待的时间为师徒二人把所有剪纸都剪完的时间。所以剪纸顺序不是重点，重点是分配任务给两人，尽量让两人同时开始同时结束，这样两人没有闲置时间是利用率最高的，总体所耗时间也是最少的。设徒弟的效率为2，则师傅的效率为2×1.5=3。6种剪纸的工作量分别为徒弟效率×徒弟所需时间，即4、12、20、24、30、50分钟。考虑若两人正好同时开工同时结束所需要时间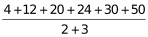：=28，但由于不能两人同时剪一个剪纸，所以不能保证就一定能分配成两个人的任务量都是28，但目前已知每个人分配的任务时间应尽量接近28分钟（因为两个人的时间和肯定是师傅时间+徒弟时间=28×2，最后一个人等待的时间为取师傅时间、徒弟时间中的最大值，师傅时间和徒弟时间越接近，两者中最大值越小）。进行任务分配：

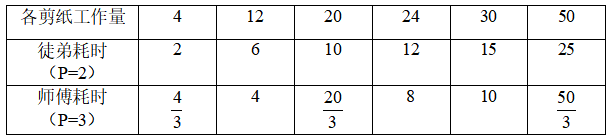
徒弟时间截为整数，现用徒弟各任务时间尽量拼凑接近28的时间量，发现6+10+12=28分钟，则剩下的工作量交给师傅为28×2-28=28分钟，取两者（28与28）最大值为28分钟。

因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。