2021年江苏省公务员考试《行测》（A卷）56

2021-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

概率问题。该题涉及环形排列：

方法一：计算总的基本事件数：基本要求是：同一个部门的人必须相邻可以采用捆绑法，将每个部门的捆绑成一个整体，则此时只有4个整体在参与一个圆形的排列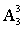，每个整体的内部排序都是，即。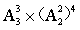

计算符合条件的事件数：额外要求为非同一个部门的小李和小王相邻，这两个人相邻需要考虑两人的相对位置即2（左右调换两种情况，或可以以一人为坐标，易发现两人相对位置只有两种，一种是在参照者左边，一种是在参照者右边）。该两人相邻而做后与小李、小王同部门的另外两人座位即自动确定。此时仍需要同一个部门的人必须相邻，采用捆绑法，小李、小王所在的两个部门相对位置已固定，这两个部门看做一个整体，另外两个部门看做两个整体，总共3个整体在环形排列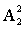：，内部排序，小李、小王所在的两个部门内部排序已考虑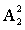（）另外两部门各自内部排序均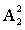为，则整体为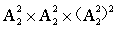（即小李、小王两部门排序×三个整体排序×另外两部门内部排序）。

计算概率：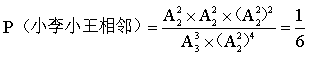

方法二：先让小李随便坐一个位置，再让小王去找小李。小李选定一个位置的概率为1，在小李旁边的两个位置中必有一个是其同部门的同事，小王只有1个位置可选，所以小王从剩下的6个空位置中选择小李旁边空位的概率为。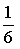

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。