2018年国家公务员考试《行测》真题卷（副省级）68

2017-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】
排列组合问题。

方法一：根据“每人值班2天，且同一人不连续值班2天”可知可用插空法解题。要求乙两天值班不连续，则将乙插入两个甲形成的三个空中，共有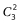种情况，此时共有两甲两乙，形成5个空位，接着再将要求不相邻的丙随机插入上述的5个空位中，共有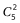种，根据“分步用乘法”原理，可知共有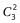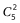=30种不同的安排方式。

因此，答案为C。

方法二：根据“甲、乙和丙三人被安排在10月1号到6号值班”，3人安排在6天值班，天数较少且情况较复杂，可采用枚举法。首先安排10月1日，甲、乙、丙三人中随机选一人，有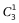种情况，然后安排10月2日，在剩余两人在选一人，有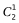种情况，10月3日-6日情况需画图枚举，如下：

假设10月1日为甲值班，2日为乙值班，则3-6日共有上图5种情况，根据“分步用乘法”原理，可知共有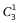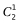×5=30种不同的安排方式。

因此，答案为C。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。