2018年国家公务员考试《行测》真题卷（副省级）67

2017-12-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】
最值问题。根据“在A、B、C、D四个城市建设72个充电站”求C市至少建设多少个充电站可知，本题考查最值问题里的和定最值问题。根据“B市建设充电站的数量占总数的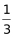”可知，B市建设充电站的数量为72×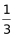=24个。又因“在C市建设的充电站数量比A市多6个，在D市建设的充电站数量少于其他任一城市”，则四个城市充电站个数关系为：B市24个，C市比A市多，A市第三多，D市最少。要使C市建设的充电站尽量少，就要让其他市建设的充电站尽量多，D市尽量多且比A市少，则D市最多为A市数量-1，已知“C市建设的充电站数量比A市多6个”，即A=C-6，则D最多为（C-7）。则A+B+C+D=（C-6）+24+C+（C-7）=72，解得C≈20.3，问至少，应向上取整，所以C至少建设21个充电站。

因此，答案为D。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。