2017年上半年（B类）待修52

2018-01-01 00:00 编辑: 高顿公考来源: 上岸鸭公考

【思路】

概率问题。

第一步，分析题干。

本题问某问题的概率，概率公式为：

，
或满足条件的概率=1-不满足条件的概率。

第二步，代入题干数据计算。

比赛进行了7局，甲获胜，那么甲至少胜了5局，最多败了2局，且最后一局一定是甲胜。

若要甲至少连胜三局，那么存在甲连胜三局、连胜四局、连胜五局三种情况；而不满足条件的情况为甲至多连赢两局，即甲连胜一局、甲连胜两局。

可见，不满足条件的情况比较好列举。

甲连胜一局即胜局彼此都不相邻，此时甲的胜负情况只有一种“胜、负、胜、负、胜、负、胜”。

甲连胜两局且最后一局胜，故前6局赢了4局，

满足条件甲至少连胜三局时，有甲连胜三局、连胜四局、连胜五局三种情况；而不满足条件的情况为甲连胜两局、连胜一局。可见，不满足条件的情况比较简单，可由反向入手。

计算总情况数：由于只打了7局，故甲胜了5局输了2局并且最后一局为甲胜，所以前面6局赢了4局，故总情况数为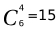种。

计算不满足条件的情况数：由于甲只输了2场，故不可能出现只连赢一场的情况（连赢一场实际上是胜局彼此都不相邻，赢一场就输一场的间隔）故甲只能是有两次连赢2场，一次连赢一场，连赢情况有“1、2、2”，“2、1、2”，“2、2、1”共三种情况。

故不满足问题条件的概率=

那么满足问题条件的概率=

因此，答案为A。

2、经本网站合法授权的，应在授权范围内使用，且使用时必须注明“来源上岸鸭公考”。违反上述声明者，本网站将依法追究其法律责任。

3、本网站的部分资料转载自互联网，均尽力标明作者和出处。本网站转载的目的在于传递更多信息，并不意味着赞同其观点或证实其描述，本网站不对其真实性负责。

4、如您认为本网站刊载作品涉及版权等问题，请与本网站联系(邮箱lihui@gaodun.com，电话：400-600-8011)，本网站核实确认后会尽快予以处理。